

If it's easier, you can start by solving an equation for To either equation to find the corresponding (The two equations represent the same line.) The lines intersect at infinitely many points. The lines intersect at exactly one point. , the graph of a system of two equations is a pair of lines in the plane. Is just a set of two or more linear equations. \[\Rightarrow \displaystyle x=2\cdot \left(-\frac\).Solving Systems of Linear Equations Using Substitution Now plugging this back into the other equation: Step 4: Plugging back to find the other variable Then, solving for \(y\), by dividing both sides of the equation by \(8\), the following is obtained Putting \(y\) on the left hand side and the constants on the right hand side we get

Now, we need to plug the substitution \(\displaystyle x=2y+2\) found from the second equation, into the first equation \(\displaystyle 3x+2y=3\), so we find that: Step 2: Plug the substitution in the other equation Putting \(x\) on the left hand side and \(y\) and the constant on the right hand side we get We use the second equation to solve for \(x\), to find a substitution: \displaystyle 3x+2y & = & 3\\\\\displaystyle x-2y & = & 2įind its solution using the substitution method. Question: Consider the following system of equation. Example: Solving a system using the substitution method The "plugging back" method, but that did not stick.
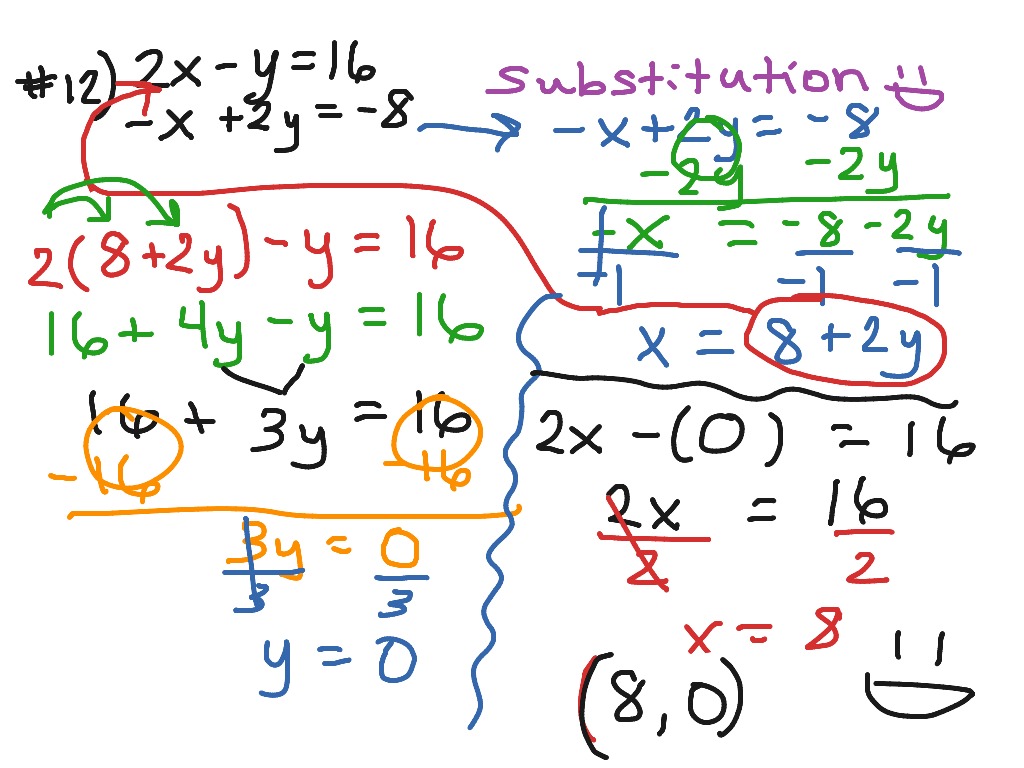
That is why it is called the substitution method. That is the substitution.Īnd then, you take the substitution and plug it into the other equation.

The name suggests directly the procedure followed: you need to find one substitution, which is obtained by using one of the equations to solve One you have typed the two equations, our calculator will try to select the best variable to do the substitution, and the plug that substitutionīack into the other equation. With this calculator, all you have to do is to type your system by specifying two linear equations.Ĭould be simplified or not, but as long as the equations are valid linear equations, it will work fine. Lots of people as about how do you solve a system of equations on a calculator, but it happens that all systems work differently. Numerically How do you do substitution on a calculator? Often times equations are given as for example "\(x = 2y + 3\)" where it is already solved for \(x\) or for example "\(y = 2x + 3\)" where it is alreadyĢ) Now that you have solved for one variable in one of the equation, use that variable you solve for, and plug it in the other equation.ģ) This equation will be in terms of the other variable (not the one you original solved for), and then you will solve for it, and you will getĤ) With the numeric result found for the other variable, come back you the original variable you solve for, and plug in the value you just solved How do you solve system of equations by substitution?ġ) Choose one of the two equations, for which it is easy to solve for any \(x\) or \(y\), and solve for that variable, If you have more than two variables or two equations, use this general system of equations calculator.Make sure to write linear equations with two variables.There are two boxes for you to write equations.
Solve by substitution how to#
How to use this Substitution calculator with steps The substitution method is a methodology to solve systems of equations that will find the solutions analytically, and it will The exact solution, you get mostly all the times an approximated solution. Representation of the equations as lines and the solution of the systemīut the problem with the graphical method is that it does not always give you Graphing method which are useful because they give you a graphical In the case of a 2 by 2 linear systems, there are approaches like the There are different approaches to solve systems of equations. More about the substitution method to solve linear systems


 0 kommentar(er)
0 kommentar(er)
